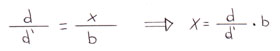Molto spesso, anzicché fotografare un oggetto da due punti, posti a distanza pari a quella interpupillare, si ricorre a distanze maggiori di questa. Questo è dovuto al fatto che il sistema di rilevamento del nostro cervello, infallibile per distanze inferiori al metro, è praticamente inutilizzabile nei rilevamenti a grande distanza.
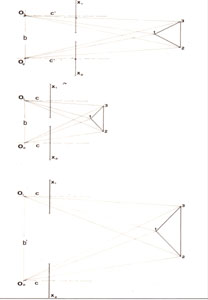
Per distanze maggiori a quella interpupillare, si ottiene un oggetto tridimensionale più ingrandito - come si può notare nell'immagine sotto riportata -, con un effetto di profondità, ottenibile sotto lo stereoscopio, maggiore; ciò permette la visione di un numero maggiore di particolari:

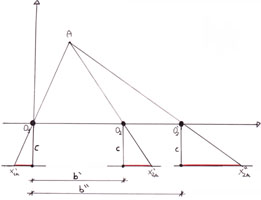b'=6 cm (distanza interpupillare) b''>b' 01, 02, 02' = punti di ripresa c = distanza principale b'' = base

Possiamo ritenere che la precisione del metodo dipende, essenzialmente, dal rapporto tra la distanza reciproca dei punti di osservazione e la distanza dell'oggetto da rilevare.
Considerando che la distanza interpupillare si aggira intorno a 6-7 cm e che la distanza minima di osservazione è mediamente di 25 cm, possiamo affermare che la precisione di rilevamento è massima quando tale rapporto assume valori intorno a 0,24 - 0,28, e minima per valori di 0,06 - 0,07, non è accettabile per valori inferiori.
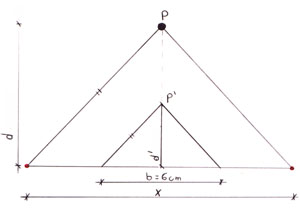
Tutto il metodo si basa nel voler osservare ad una distanza d' (supponiamo 30 cm), un oggetto, P, posto alla distanza d>d'; la distanza x tra i due punti di ripresa, dai quali saranno scattate le due foto, si ottiene dalla seguente proporzione, che sfrutta la similitudine dei due triangoli:
Ecco alcune trasformazioni del modello ottico che si possono ottenere:

- aumentando o riducendo la base, b, a parità di distanza principale, c, e di fotogrammi, il modello viene ingrandito o rimpicciolito, ma le proporzioni restano inalterate;   - aumentando o diminuendo la distanza principale, a parità di base e di fotogrammi, quindi alterando l'orientamento dei raggi proiettanti, il modello viene allungato o accorciato.