LA FOTOGRAMMETRIA ARCHITETTONICA   La fotogrammetria architettonica è una tecnica che consente di rilevare le misure dell'organismo architettonico dalle immagini fotografiche dello stesso.   I principi su cui si basa tale tecnica sono i seguenti:  - un qualsiasi punto P della superficie di un oggetto emette un fascio di raggi luminosi;  - uno di questi raggi, attraverso l'obiettivo della macchina fotografica (identificato con il centro di proiezione), secondo una traiettoria rettilinea, proietta l'immagine P1 del punto sulla superficie sensibile;  - invertendo il processo di proiezione, l'immagine P1 del punto si proietta sul punto reale P;  - ripetendo l'esperienza con due macchine fotografiche, poste ad una certa distanza (che chiamiamo "base"), i raggi proiettanti le immagini P1 e P2 del punto P si intersecano nel punto stesso.   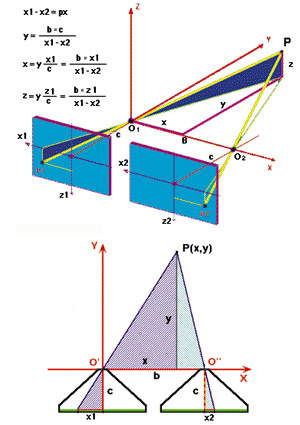Nella figura riportata è rappresentato lo schema geometrico di quello che comunemente viene definito il "caso normale", in cui le superfici sensibili sono complanari e gli assi ottici degli obiettivi sono perpendicolari ad esse (e quindi paralleli tra loro).   Sfruttando la similitudine dei triangoli determinati dai raggi proiettanti il punto P, si trova una corrispondenza biunivoca tra le coordinate (x,y,z) di P nel riferimento cartesiano (O1,x,y,z) e le due coppie di coordinate (x1,z1), (x2,z2) delle immagini P1 e P2 nei riferimenti (x1,z1) e (x2,z2) fissati sui due fotogrammi.   Come si vede, l'origine di ciascuno dei due sistemi, esistenti sui fotogrammi, si trova nel punto di intersezione del fotogramma con la perpendicolare condotta dal centro di proiezione alla superficie del fotogramma stesso. Questo punto prende il nome di "punto principale". Gli assi delle ascisse (x1 e x2) e delle ordinate (z1 e z2) degli stessi sistemi, essendo l'immagine capovolta, sono diretti rispettivamente verso sinistra e verso il basso. La distanza C del centro di proiezione dalla superficie del fotogramma è detta "distanza principale".   Dalle formule riportate si deduce inoltre che le coordinate (x,y,z) del punto P sono funzioni lineari della base B. Pertanto se si mantengono inalterate le altre variabili (x1,z1,x2,z2), il modello ottico steremetrico ottenuto ha la stessa scala di rappresentazione della base, cioè aumentando o riducendo quest'ultima, il modello si ingrandisce o si rimpicciolisce mantenendo le proporzioni inalterate.

Bibliografia Antonio Daddabbo - "Il rilievo stereofotogrammetrico" - Levante Editori-Bari Antonio Daddabbo - "Fotogrammetria e tutela del territorio" - Levante Editori-Bari