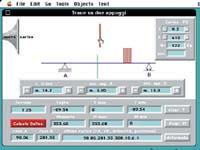
L’uso del computer, visto come strumento programmabile, destinato a svolgere rapidamente tutte quelle azioni ripetitive che spesso distraggono lo studente dall’obiettivo prefisso, non può considerarsi "alternativo" all’uso della calcolatrice: oltre che richiedere "negli alunni l'esercizio della riflessione e del ragionamento", il computer consente, in ogni momento, qualsiasi verifica delle operazioni svolte e ciò rappresenta il vero stimolo nello studio. Lo studio della Geometria elementare rappresenta un’ottima occasione per avviare lo studente alla programmazione. Inizialmente la rappresentazione di una retta richiederà un tempo superiore a quello richiesto in passato, ma lo studente sarà gratificato dalla verifica fornita in tempo reale dal computer, mentre la stessa visualizzazione grafica consentirà di chiarire molti concetti. Il programma, sopra riportato, riguarda la risoluzione di una trave su due appoggi e consente la rappresentazione grafica della trave, dei vincoli e dei carichi. Per ogni carico aggiunto, è possibile conoscere subito il nuovo valore delle reazioni agli appoggi e il valore delle sollecitazioni in una sezione prescelta. Con un clic sul pulsante "Calcolo sollec." è possibile avviare l’analisi continua delle sollecitazioni in tutte le sezioni della trave, leggendo i valori sia sotto forma grafica che numerica. Tutto ciò è il risultato del lavoro di tre anni, che sono stati necessari per assimilare non solo il linguaggio di programmazione, ma per comunicare alcuni concetti di statica. L’enorme vantaggio del computer è dato non tanto dalla sua capacità di memorizzare le operazioni, quanto dalla possibilità di consentire continuamente le modifiche necessarie. Nella figura soprastante viene riportata la versione successiva del programma visto. Non è difficile notare come l’attenzione del programmatore si sia spostata sempre più verso i contenuti numerici: nelle prime due videate vengono inseriti i dati, mentre la terza videata è stata riservata alla illustrazione dei risultati. E’ da precisare, ancora una volta, che un simile programma è partito dalla semplice risoluzione di una trave isostatica su due appoggi con un carico concentrato. In seguito il problema è stato generalizzato, rendendo il carico mobile e ripartito, quindi è stata data la possibilità di spostare gli appoggi; ma ogni operazione è stata sempre la conseguenza della conoscenza di nuove possibilità di calcolo e della memorizzazione di nuove formule. Nelle figure di questa pagina sono riportati i programmi relativi al calcolo e verifica di un pilastro soggetto a carico di punta e alle percentuali della miscela degli inerti. Risulta evidente come, noti i valori e le leggi di variazione, questo tipo di programmazione possa essere svolto dal docente di matematica, che senza far ricorso ad apposite e spesso inconcludenti riunioni collegiali, soddisfa le richieste ministeriali sul coordinamento interdisciplinare. Il programma mostrato in questa pagina è un esempio di quello che potrebbe essere il primo passo per la realizzazione del "manuale personale" di ogni studente. Si tratta della classica raccolta di formule che ogni studente utilizza di nascosto nei compiti in classe e che, in questo caso, hanno dato "vita" ad una serie di strumenti appartenenti ad un piano di lavoro elettronico e richiamabili da menu, su finestre galleggianti. Il linguaggio di programmazione è sempre HyperTalk, ampiamente trattato nel volume "Cartografia digitale in architettura e urbanistica" (Levante Editori - Bari), e tutto il programma sfrutta la possibilità di conoscere le coordinate del cursore con un semplice "click". Ciò fatto, tutto si riduce alla risoluzione di triangoli ed al cambiamento del sistema di riferimento. Probabilmente più di un docente, nell’esaminare un simile programma, pronuncia la fatidica frase "Troppo comodo!". Tralasciando ogni commento, occorre far presente che l’impiego di una formula non si riduce alla semplice operazione matematica, perché i guai cominciano proprio dall’esame dei risultati. Prendiamo in esame lo strumento più semplice, il "distanziometro", utilizzato per rilevare la distanza tra due punti di una cartografia riportata sul nostro piano di lavoro. Fare click in due punti indicati dal cursore, memorizzare le coordinate, applicare la formula della distanza e mostrare il risultato sul video richiede probabilmente lo stesso tempo necessario per misurare la distanza stessa con uno scalimetro, su una cartografia tradizionale. La differenza comincia a evidenziarsi quando l’operazione si ripete; per esempio, per il calcolo della lunghezza di una poligonale, con la cartografia digitale l’incremento di tempo è sempre quello corrispondente al "click", mentre nel caso del supporto cartaceo, anche se con l’ausilio di una calcolatrice, i tempi aumentano e con essi la possibilità di commettere errori! Non va trascurato il fatto che il supporto cartaceo è soggetto a dilatazione, per cui risulta ridicolo apprezzare su di esso la frazione di millimetro. La cartografia digitale non è soggetta a dilatazione e questo già può alimentare la speranza di migliorare la precisione della misura. Si scopre così che effettuare il passaggio da pixels a metri prima o dopo il calcolo della distanza non è la stessa cosa e importanza fondamentale assume la risoluzione dello schermo. Quando, infine, si è convinti di avere a che fare con un errore sistematico e si ha bisogno di una misura per la taratura della carta, si scopre che non esiste una carta degna di... fiducia! Questa semplice constatazione può rappresentare l’occasione per avviare quella "ricerca personale di aggiornamento", cui fanno riferimento i programmi ministeriali.