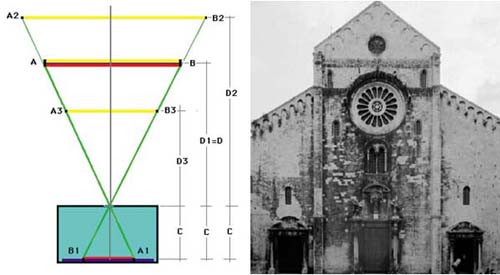
If we photograph a flat surface (or which, however, can be considered as such) respecting the parallelism between the plane containing the sensitive material and the surface itself, the photographic image will be the scaled representation of the considered surface.
In the figure a horizontal section is taken into consideration: the segment AB will project itself into the segment A1B1. By inverting the direction of projection, the photographic image will be projected on the segment itself AB, if the risen distance D will be equal to that of projection D1, otherwise it will have a greater or lesser size according to whether the projection distance will be greater or less than that of shot D. From the figure it is easy to deduce that, thanks to the similarity of the triangles having the center of projection as their vertex, the photographic image is reproduced on a scale equal to the ratio between the main distance C and the shooting distance D. With the same logic it is possible to derive the relationship (and therefore the scale) between the photographic image (negative) and its projection (positive).